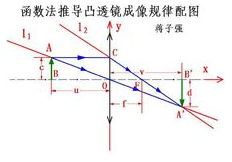
【题】 如右图 ，用函数法证明1/u+1/v=1/f。

　　【解】右图为凸透镜成像示意图。

　　其中c为成像的物体长度，d为物体成的像的长度。u为物距，v为像距，f为焦距。

　　步骤

　　(一)为便于用函数法解决此问题，将凸透镜的主光轴与平面直角坐标系的横坐标轴(x轴)关联(即重合)，将凸透镜的理想折射面与纵坐标轴(y轴)关联，将凸透镜的光心与坐标原点关联。则：点A的坐标为(-u,c)，点F的坐标为(f,0)，点A'的坐标为(v,-d)，点C的坐标为(0，c)。

　　(二)将AA’，A'C双向延长为直线l1,l2，视作两条函数图象。由图象可知：直线l1为正比例函数图象，直线l2为一次函数图象。

　　(三)设直线l1的解析式为y=k1x,直线l2的解析式为y=k2x+b

　　依题意，将A(-u,c),C(0,c),F(f,0)代入相应解析式得方程组：

　　c=-u·k1

　　c=b

　　0=k2f+b

　　把k1,k2当成未知数解之得：

　　k1=-(c/u), k2=-(c/f)

　　∴两函数解析式为：

　　y=-(c/u)x, y=-(c/f)x+c

　　∴两函数交点A'的坐标(x,y)符合方程组

　　y=-(c/u)x

　　y=-(c/f)x+c

　　∵A'(v,-d)

　　∴代入得：

　　-d=-(c/u)v

　　-d=-(c/f)v+c

　　∴-(c/u)v=-(c/f)v+c=-d

　　∴(c/u)v=(c/f)v-c=d

　　cv/u=(cv/f)-c

　　fcv=ucv-ucf

　　fv=uv-uf

　　∵uvf≠0

　　∴fv/uvf=(uv/uvf)-(uf/uvf)

　　∴1/u=1/f-1/v

　　即：1/u+1/v=1/f