2018.03.19 15:23
新东方在线中考网整理了《2018中考数学压轴题(38)》,供同学们和家长参考。
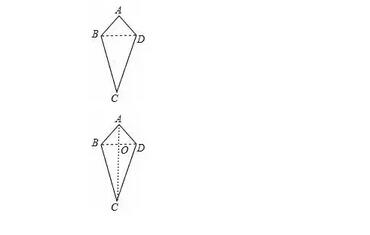
研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
(1)小文认为菱形是特殊的“筝形”,你认为他的判断正确吗?
(2)小文根据学习几何图形的经验,通过观察、实验、归纳、类比、猜想、证明等方法,对AB≠BC的“筝形”的性质和判定方法进行了探究.下面是小文探究的过程,请补充完成:
①他首先发现了这类“筝形”有一组对角相等,并进行了证明,请你完成小文的证明过程.
已知:如图,在”筝形”ABCD中,AB=AD,CB=CD.
求证:∠ABC=∠ADC.
证明:
②小文由①得到了这类“筝形”角的性质,他进一步探究发现这类“筝形”还具有其它性质,请再写出这类“筝形”的一条性质(除“筝形”的定义外) ;
③继性质探究后,小文探究了这类“筝形”的判定方法,写出这类“筝形”的一条判定方法(除“筝形”的定义外):

②“筝形”有一条对角线平分一组对角(答案不唯一),
连接AC,BD,
∵AB=AD,
∴A在BD的垂直平分线上,
∵BC=DC,
∴C在BD的垂直平分线上,
∴AC是BD的垂直平分线,
∵AB=AD,BC=CD,
∴AC平分∠BAC和∠BCD,
∴“筝形”有一条对角线平分一组对角,
故答案为:“筝形”有一条对角线平分一组对角;
③有一条对角线垂直平分另一条对角线的四边形是筝形(答案不唯一).
故答案为:有一条对角线垂直平分另一条对角线的四边形是筝形.
考点分析:
四边形综合题.
题干分析:
(1)菱形四边相等,根据筝形定义可得菱形是特殊的“筝形”;
(2)①连结BD,根据等边对等角可得∠ABD=∠ADB,∠DBC=∠BDC,进而可得∠ABC=∠ADC;
②连接AC,BD,根据线段垂直平分线的判定可得AC是BD的垂直平分线,根据等腰三角形三线合一的性质可得AC平分∠BAC和∠BCD;
③根据线段垂直平分线的性质可得如果AC是BD的垂直平分线,则AB=AD,BC=CD.
解题反思:
此题主要考查了四边形的综合,关键是掌握等腰三角形的性质,以及等腰三角形的判定:等边对等角.到线段两端点距离相等的点在线段的垂直平分线上.
更多中考资料下载、中考最新资讯、中考录取分数、中考体育等最新中考信息,请关注新东方在线中考网。
相关推荐:
| 8科2018中考复习资料大全(下载版) | ||
| 序号 | 2018中考复习资料大全 | 查看详情 |
| 1 | 2018中考语文复习资料大全(下载版) | 点击查看 |
| 2 | 2018中考数学资料大全(下载版) | 点击查看 |
| 3 | 2018中考英语复习资料大全(下载版) | 点击查看 |
| 4 | 2018中考物理资料大全(下载版) | 点击查看 |
| 5 | 2018中考化学复习资料大全(下载版) | 点击查看 |
| 6 | 2018中考地理复习资料大全(下载版) | 点击查看 |
| 7 | 2018中考历史复习资料大全(下载版) | 点击查看 |
| 8 | 2018中考政治复习资料大全(下载版) | 点击查看 |

扫码预约一对一精华课
资深教师+1对1定制教学

