【题目】
41.(10分)设有6个有序表A、B、C、D、E、F,分别含有10、35、40、50、60和200个数据元素,各表中元素按升序排列。要求通过5次两两合并,将6个表最终合并成1个升序表,并在最坏情况下比较的总次数达到最小。请回答下列问题。
(1)给出完整的合并过程,并求出最坏情况下比较的总次数。
(2)根据你的合并过程,描述n(n≥2)个不等长升序表的合并策略,并说明理由。
【答案要点】:
(1)6个表的合并顺序如下页图所示。
根据下页图中的哈夫曼树,6个序列的合并过程为:
第1次合并:表A与表B合并,生成含45个元素的表AB;
第2次合并:表AB与表C合并,生成含85个元素的表ABC;
第3次合并:表D与表E合并,生成含110个元素的表DE;
第4次合并:表ABC与表DE合并,生成含195个元素的表ABCDE;
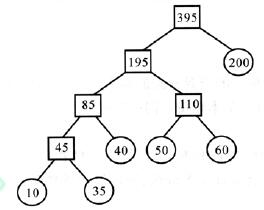
对应于合并过程的哈夫曼树
第5次合并:表ABCDE与表F合并,生成含395个元素的最终表。(5分)
由于合并两个长度分别为m和n的有序表,最坏情况下需要比较m+n-1次,故最坏情况下
比较的总次数计算如下:
第1次合并:最多比较次数=10+35-1=44
第2次合并:最多比较次数=45+40-1=84
第3次合并:最多比较次数=50+60-1=109
第4次合并:最多比较次数=85+110-1=194
第5次合并:最多比较次数=195+200-1=394
比较的总次数最多为:44+84+109+194+394=825。(2分)
(2)各表的合并策略是:在对多个有序表进行两两合并时,若表长不同,则最坏情况下总的比较次数依赖于表的合并次序。可以借用哈夫曼树的构造思想,依次选择最短的两个表进行合并,可以获得最坏情况下最佳的合并效率。(3分)