2020年计算机考研复习已经开始,新东方在线在此整理了2020考研计算机组成原理知识点:定点数的表示和运算,希望能帮助大家!
定点数的表示和运算
1. 定点数的表示
1)无符号数的表示
无符号数就是指正整数,机器字长的全部位数均用来表示数值的大小,相当于数的绝对值。
对于字长为n+1位的无符号数的表示范围为:

2. 定点数的运算
1)定点数的位移运算
左移,绝对值扩大;右移,绝对值缩小。
算术移位规则
符号位不变

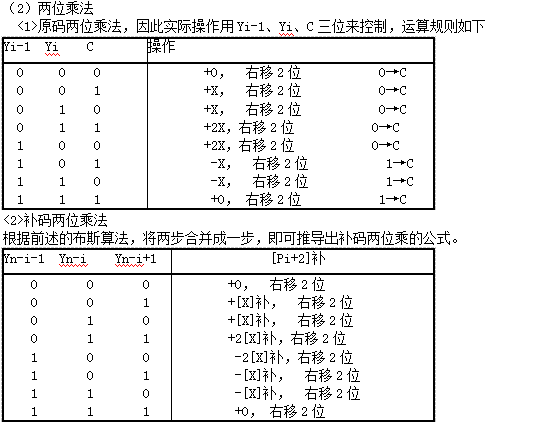
求部分积的次数和右移操作的控制问题。
当乘数由1位符号位和以n(奇数)位数据位组成时,求部分积的次数为(1+n)/2,而且最后一次的右移操作只右移一位。
若数值位本身为偶数n,可采用下述两种方法之一:
①可在乘数的最后一位补一个0,乘数的数据位就成为奇数,而且其值不变,求部分积的次数为1+(n+l)/2,即n/2+1,最后一次右移操作也只右移一位。
②乘数增加一位符号位,使总位数仍为偶数,此时求部分积的次数为n/2+1,而且最后一次不再执行右移操作。
(3)补码除法
<1>定点原码一位除法
1>恢复余数法
被除数(余数)减去除数,如果为0或者为正值时,上商为1,不恢复余数;如果结果为负,上商为0,再将除数加到余数中,恢复余数。余数左移1位。
2>加减交替法
当余数为正时,商上1,求下一位商的办法,余数左移一位,再减去除数;当余数为负时,商上0,求下一位商的办法,余数左移一位,再加上除数。
<2>定点补码一位除法(加减交替法)
1〉如果被除数与除数同号,用被除数减去除数;若两数异号,被除数加上除数。如果所得余数与除数同号商上1,否则,商上0,该商为结果的符号位。
2〉求商的数值部分。如果上次商上1,将除数左移一位后减去除数;如果上次商上0,将余数左移一位后加除数。然后判断本次操作后的余数,如果余数与除数同号商上1,如果余数与除数异号商上0。如此重复执行n-1次(设数值部分n位)。
3〉商的最后一位一般采用恒置1的办法,并省略了最低+1的操作。此时最大的误差为2-n。
5)溢出概念和判别方法
当运算结果超出机器数所能表示的范围时,称为溢出。显然,两个异号数相加或两个同号数相减,其结果是不会溢出的。仅当两个同号数相加或者两个异号数相减时,才有可能发溢出的情况,一旦溢出,运算结果就不正确了,因此必须将溢出的情况检查出来。判别方法有三种:
1〉当符号相同的两数相加时,如果结果的符号与加数(或被加数)不相同,则为溢出。
2〉当任意符号两数相加时,如果C=Cf,运算结果正确,其中C为数值最高位的进位,Cf为符号位的进位。如果C≠Cf ,则为溢出,所以溢出条件=C⊕Cf 。
3〉采用双符号fs2fs1。正数的双符号位为00,负数的双符号位为11。符号位参与运算,当结果的两个符号位甲和乙不相同时,为溢出。所以溢出条件= fs2⊕fs1 ,或者溢出条件= fs2fs1 + fs2fs1